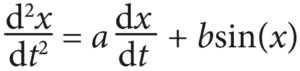Hybrid Continuous-Discrete Computers
for Cyber-Physical Systems

Funded by the National Science Foundation

Grant Awards #1239134 and #1239136

Description

The goal of this research is to investigate and demonstrate the capabilities of hybrid computers, combining both discrete and continuous computation, in the context of cyber-physical systems. This goal is to be reached through research in several areas: (1) Hardware: we use modern silicon chip technology to bypass the problems that plagued analog computers in the past, merging analog computing hardware on the same chip with digital hardware, the latter used for control and co-computation, (2) Architecture: we devise methods for making computing functionality accessible to the software, (3) Microarchitecture: This involves choices on the granularity, type and organization of analog and hybrid functional units, and (4) Application to a realistic cyber-physical system. This is a collaborative project between researchers from Columbia University and The University of Texas at Austin.

Principal and Scope Investigators

Students

PhD Students:

Ning Guo (Analog Design)
Yipeng Huang (Architecture and Software)
Sharvil Patil (ADC Design)
Yu Chen
Doyun Kim

MS Students:

Zhe Cao
Tao Mai

Publications & Presentations

Applications

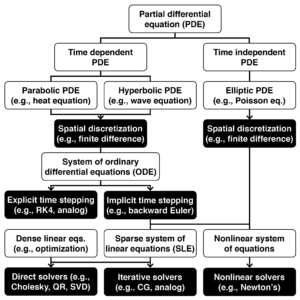
We explore hybrid computer applications in two areas that rely on continuous mathematics: cyber-physical systems and high-performance computing. These include applications that rely on ordinary differential equations (ODEs), linear algebra, and systems of nonlinear equations.

Applications: Ordinary differential equations

The most natural application of hybrid analog-digital co-processors is in solving ODEs, such as the one shown here:

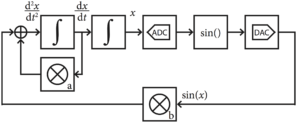
The analog co-processor sets up a electrical circuit, below, whose output variables’ behavior over time is described as an ODE.

The integrators are charged to an initial value. Upon release, the variable x is solved according to the ODE. This way of using analog co-processors is most useful in small-scale ODE solvers, such as those needed in robotics and Internet-of-things devices. It is especially useful when the input to the computer is analog, and the desired output is also analog, therefore eliminating the need to do A/D/A conversion. We have demonstrated that such an approach can achieve 1,000 times performance speedup.

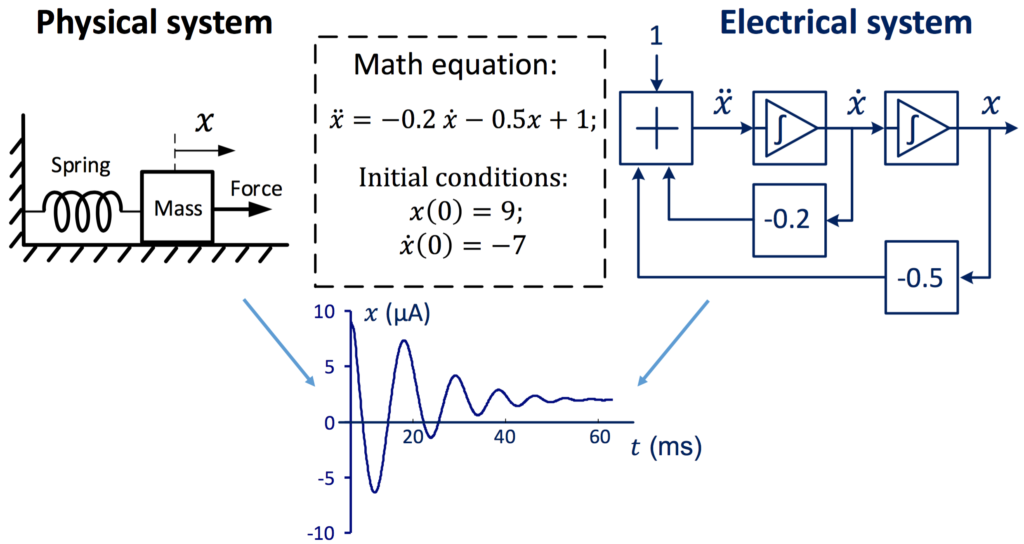
Using this basic idea, an analog computer can solve the ODE that describes a physical system. Here, the analog computer simulates a mass-spring-damper system:

It can also solve ODEs in cyber-physical systems, such as two-wheeled mobile robots:

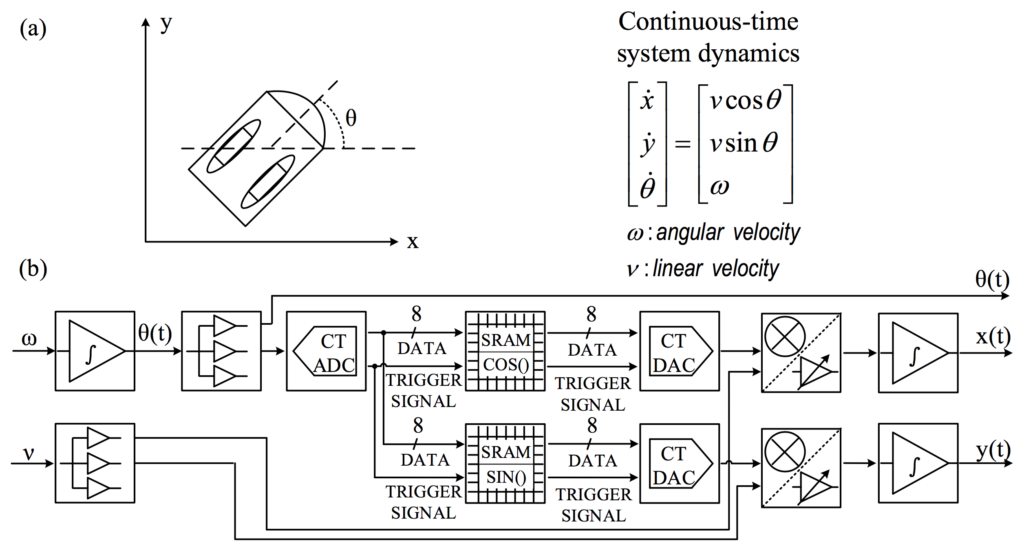
Applications: Linear Algebra

Since many HPC applications decompose down to linear algebra problems, it is natural to attempt to solve sparse systems of linear equations on an analog co-processor. Analog co-processors can do this by doing iterative methods for numerical linear algebra, namely, steepest gradient descent, in continuous-time. This approach of solving sparse linear algebra has the advantage of solving a class of problems much more widely occurring than ODEs.

How feedback in an analog computer circuit can be used to implement scalar division (left) and solving for the solution vector of a linear algebra problem (right). Analog computers can use negative feedback to compute quotients: ax–b = 0. As long as a is positive, the circuit here has x tending toward the stable solution x = b/a, at which point the summing point at the input of the integrator becomes zero. This technique can solve linear algebra problems, Ax–b = 0. Using a vector of integrators and a matrix of multipliers, the circuit here has the integrators’ output tend toward x = A^-1b, as long as A is positive definite.

When linear algebra is the class of problems that we solve in analog co-processors, several drawbacks of analog computing can be handled:

Sampling precision: the solution to the linear algebra problem is the steady-state output of the analog computer. Since it is stable in time, we can sample it to high precision, without having to worry about sampling frequency.
Problem size: sparse linear algebra problems can be decomposed into multiple smaller problems, each of which can fit in the hardware size of an analog co-processor.
Dynamic range of variables: the dynamic range of the variables in the equation can be scaled to fit in the dynamic range of analog variable. Since the systems of equations are linear, the coefficients and variables of the equations can be divided by a common scaling factor.

Prior work done at Columbia University on solving linear algebra problems on analog co-processors shows that such an approach may have 10 times better performance than digital methods, while spending 1/3 less energy. The team found that analog co-processors for linear algebra must offer high analog bandwidth in order to speed up convergence of the circuit. Providing this analog bandwidth in the circuit consumes silicon area and increases power consumption.

Programming & Architecture

Programming model

We have built two programming approaches to the prototype HCDC: 1. A graphical, spatial approach to connecting the blocks. 2. A pragma that allows the HCDC to be used from within imperative code, such as a C program.

Instruction set architecture

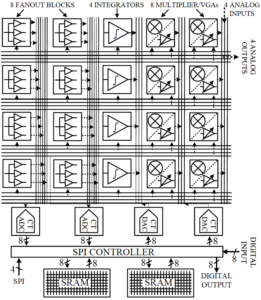
First generation chip architecture.

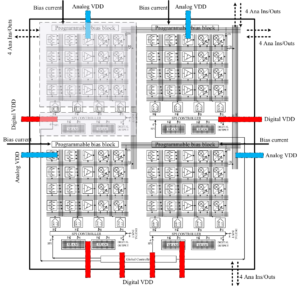
Second generation chip architecture, showing rows of analog, mixed-signal, and digital components, along with crossbar interconnect. Each of the four rows of analog components are logically organized as a macroblock. “CT” refers to continuous time. SRAMs are used as lookup tables for nonlinear functions.

The analog accelerator acts as a peripheral to a digital host processor, which provides a configuration for the analog accelerator, performs calibration, controls computation, and reads out the output values. We walk through how to use the instructions in the steps below.

Calibration: Before using the analog accelerator, the analog circuitry must first be calibrated. Numerical errors in analog computing come from three types non-ideal behaviors. 1. offset bias: a constant additive shift in values, 2. gain error: an error in how much values are multiplied, 3. nonlinearity: the possibility that the DC transfer characteristic has a non-constant slope. The effect of these non-ideal behaviors varies between function units due to process variations. We use small DACs in each block to compensate for the first two sources of error by shifting signals and adjusting gains. These DACs are controlled by registers, whose contents are set during calibration by the digital host. The settings vary across different copies of the analog accelerator chip, but remain constant during accelerator operation and between solving different problems. When an analog unit is calibrated, its inputs and outputs are connected to DACs and ADCs; then, the digital processor uses binary search to find the settings that give the most ideal behavior. The third source of error, nonlinearity, is kept under control via overflow exception detection.
Configuration: Before computation is offloaded to the accelerator, the programmer maps out the connections between analog units, along with settings of the units, and sends it to the analog accelerator using the configuration instructions. This configuration bitstream is written to digital registers on the analog accelerator. These digital registers contain only static configuration, akin to the program, and no dynamic computational data.
Computation: The architecture interface has instructions which control the start and stop of integration, which signify the beginning and end of analog computation.
Exceptions: A key aspect of the analog accelerator compared to prior analog computing designs is its ability to report exceptions. After computation is done, the chip can report if any exceptions occurred during analog computation. All analog hardware designs have a range of inputs where the output is linearly related to the input. Exceeding this range leads to clipping of the output, similar to overflow of digital number representations. The integrators and ADCs detect when their inputs exceed the linear input range, and these exceptions are reported to the digital host. At the same time, the host also observes if the dynamic range is not fully used, which may result in low precision. When such exceptions occur the original problem is scaled to fit in the dynamic range of the analog accelerator and computation is reattempted.

Microarchitecture

Our research group recently prototyped an analog chip in 65nm CMOS technology, shown in the images below.

v1_schematic — First generation chip layout.

v2_chip — Second generation chip layout.

The accelerator consists of analog functional units connected with a crossbar. Each chip is organized as four macroblocks, each macroblock consisting of one analog input from off-chip, two multipliers, one integrator, two current-copying fanout blocks, and one analog output to off-chip. Two macroblocks share use of an 8-bit ADC, an 8-bit DAC, and a nonlinear function lookup table (256-deep, 8-bit continuous-time SRAM). The chip also includes an interface to receive commands from the main digital processor. In the prototype these commands are received over an interface implementing an SPI protocol.

In our analog accelerator, electrical currents represent variables. Fanout current mirrors allow copying variables by replicating values onto different branches. To sum variables, currents are added together by joining branches. Eight multipliers allow variable-variable and constant-variable multiplication. The variables can also be subjected to arbitrary nonlinear functions, such as sine, signum, and sigmoid with the SRAM lookup table.

Overflow detection is done using analog voltage comparators to detect values exceeding the safe range. We compare a reference value (usually the maximum or minimum allowed values) to the signal carrying the variable. When a value exceeds the safe range an exception bit is set in a latch whose value can be read out during exception checking.

Literature review

Retrospective

Summary poster [pdf]

Hybrid Continuous-Discrete Computersfor Cyber-Physical Systems