As we enter the post-Moore’s law era of computing, researchers are turning to new models of computation to address humanity’s grand challenges. These emerging models of computation include analog computing and quantum computing. At a high level, they offer fundamentally different capabilities compared to classical, digital computing machines. These capabilities include simulating natural phenomena using physics as a direct model. My research addresses the challenges in harnessing these promising models of computation: the challenges include connecting these emerging architectures to conventional von Neumann architectures and in helping programmers correctly use them.
Ph.D. dissertation research in analog acceleration
My Ph.D. dissertation at Columbia University examined hybrid analog-digital computing to support modern scientific computing workloads. My research connected applied mathematics application-level requirements to electrical engineering prototype device-level support. The core contribution of my Ph.D. research was finding that solving nonlinear algebraic equations is the best abstraction for using analog accelerators to help solve partial differential equations (PDEs). My collaborators and I built prototype analog accelerator chips that companies and other universities have since taken up for commercialization and further research. The computer architecture research community identified the importance of my work and named it one of 12 Top Picks among computer architecture conference papers in 2016 and again as an honorable mention in 2017. Furthermore, I secured funding from DARPA via a Small Business Technology Transfer (STTR) grant to assess the commercial applications of my research.
Background on continuous-time analog computing

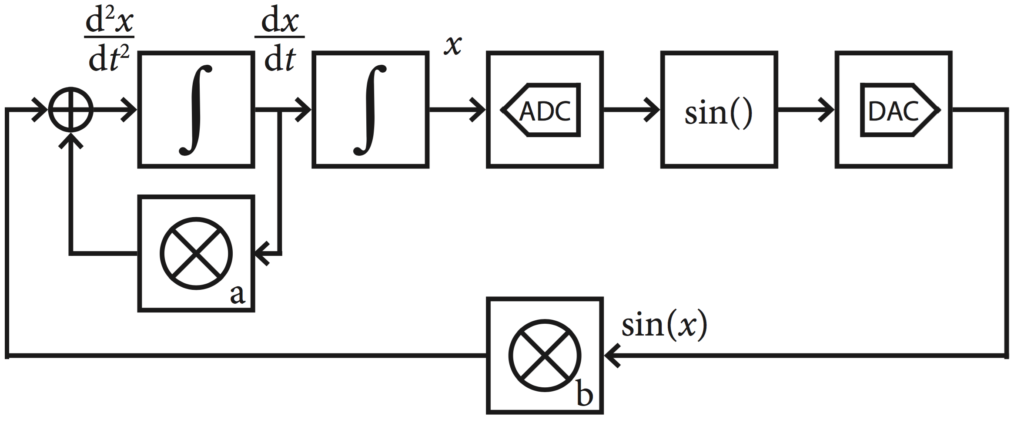
Analog computing uses the current and voltage dynamics of analog electronic circuits to simulate the physical world. Scientists model processes such as projectile trajectories as ordinary differential equations (ODEs). Analog computers solve ODEs by creating circuits whose continuous-time analog output waveforms follow the same ODEs. Analog computing was used widely in the mid-20th century—the direct mapping from problem to hardware solution offered higher performance than the nascent digital machines at that time.
Prototype analog accelerator chip

With collaborators at Columbia University, our team built two iterations of a prototype analog accelerator chip with the goal of revisiting analog computing. On that team, I led designing the instruction set architecture, building the on-chip interconnection network, synthesizing and laying out the digital control circuitry, and validating the overall functionality. The reconfigurable chip that we created comprises integrators that track the analog values that represent problem variables, multipliers for finding products of problem variables, hardware blocks for summing and copying variables, and analog/digital converters to generate parameters and obtain results. Our chip served as a critical proof-of-concept for instantiating the computational model in modern CMOS technology, and it served as a testbed for solving ODE problems that occur in cyber-physical systems (CPS). Most importantly, we were able to transfer the chip to research groups at MIT and at Ulm University interested in compiling problems to such devices and to companies interested in using the chips as low-power embedded equation solvers. Our chips will continue to serve as valuable ground truth prototypes for research in applications, algorithms, and languages for analog accelerators.
DARPA-funded applications feasibility study in scientific computing
Our prototype chip caught the attention of DARPA, who was interested in emerging architectures for scientific computation and was specifically concerned whether real-world commercial applications can run on analog accelerators. The next phase of my research was funded through an STTR grant, in which I took the lead in writing the proposal, negotiating the contract, and writing and presenting the findings to DARPA as the project’s PI.
Emerging scientific computing problems in even the most constrained embedded systems pose daunting challenges for analog accelerators. Analog accelerators offer the high performance and low power consumption ideal for CPS settings; however, they fail to support the precision and problem sizes that these applications now demand. For example, mobile robots with limited computing power and energy stores now need to solve PDEs for path planning and to model the world. Solving such problems relies on sophisticated algorithms and software stacks, and the problems have precision and problem size requirements that researchers previously associated with high-performance computing (HPC). In short, yesterday’s HPC is tomorrow’s CPS.
Key abstractions for hybrid analog-digital computation
The key to successfully support modern scientific computing problems is to use the analog accelerators to solve nonlinear systems of equations. Such an abstraction offers several benefits and mitigates the limitations of analog accelerators:
- The digital host computer divides large problems which are then conquered in the analog accelerator—Modern PDE solvers split PDEs into discrete steps in space and in time. The solvers then tackle the resulting nonlinear and linear algebra problems, which end up dominating all scientific computing workloads. Analog accelerators can support arbitrarily large problems by focusing on solving algebraic equations that do fit in the accelerator. See also: [slides]
- The analog accelerator generates approximate seed solutions which are then refined in the digital host—In order to solve algebraic equations, digital computers use iterative numerical methods that take successively better guesses at the correct solution. Those iterative numerical methods face challenges in finding good initial guesses and iteration step sizes. Analog accelerators entirely sidestep the problems by performing iterative methods, such as Newton’s method, as ODEs. The analog accelerators’ approximate solutions are then good initial guesses for digital algorithms for finding high-precision solutions. See also: [summary] [poster] [slides]
- Such a division of labor between analog and digital draws on the strengths of each, while preserving existing software and tools for solving PDEs.
The need for algorithms, compilers, and architecture research for analog and other emerging architectures.
As mentioned, the computer architecture research community recognized my papers sharing these insights as a Top Pick in 2016 and as an honorable mention in 2017. The computer science department at Columbia University nominated my work on these topics for the ACM doctoral dissertation award in 2018. My work has demonstrated the potential of analog accelerators, and it has also shown that comprehensive full-stack research in algorithms, compilers, and architecture is needed to enable their widespread application.
Postdoc research in quantum program simulation and debugging
My postdoctoral work at Princeton University continues my research in abstractions for safely using emerging computer architectures, specifically in helping researchers debug and simulate quantum programs. Quantum computing is at a critical juncture where prototype machines are now capable of running quantum algorithms. With the burgeoning interest among researchers and students to write quantum programs, the research field urgently needs tools to debug quantum programs and simulate them on classical computers.
Quantum program patterns, bugs, and debuggers
My paper at the 2019 International Symposium for Computer Architecture is the first paper to concretely describe quantum programming bugs, the symptoms they cause, and how programmers can use my open-source tools to debug their quantum programs. Quantum program debugging is a vital step toward useful quantum computing, but until recently no one had chronicled their experience in debugging concrete quantum programs. In response, I built and collected a suite of quantum programs including applications in chemistry, optimization, cryptography, and search. These programs span a representative set of quantum algorithm primitives that underlie the power of quantum algorithms. In the process of validating and debugging these programs, I categorized what types of bugs may occur, what symptoms the bugs cause, and how various quantum programming languages offer different features that prevent certain types of bugs. See also: [summary] [poster] [slides]
I developed open-source tools that help programmers debug quantum programs using assertions based on statistical tests. Debugging quantum programs is especially challenging compared to classical debugging: there is no easy way for programmers to pause programs and observe values as such observations would alter the delicate quantum program state. Even when observations are available, programmers cannot easily interpret the information decide if it is correct. I introduced quantum program assertions that allow programmers to express that the quantum state should be one of classical, superposition, or entangled states. The toolchain would then simulate or run the quantum program many times up to that breakpoint and collect an ensemble of measurements at that point. Statistical tests then determine whether the measurements are consistent with the expected state. My language extensions are in the process of being accepted into IBM’s Qiskit, the leading framework for quantum computing tutorials and experimentation.
AI probabilistic graphical models as abstractions for quantum programs
My ongoing and near-future research work is in using probabilistic graphical models (PGMs) as an abstraction to aid simulating and reasoning about quantum programs. PGMs such as Bayesian networks, Markov networks, and tensor networks originated in classical machine learning inference as models about causation in the world. PGMs have now emerged as an important program abstraction for quantum computing: with slight modifications of PGM semantics so they work with complex-valued amplitudes instead of real-valued probabilities, they can represent quantum circuits with no loss of generality. Prior work has focused only on using PGM inference techniques such as variable elimination for scaling up simulations of specific classes of quantum programs. Overall, researchers are far from fully exploiting the full power of PGMs as an abstraction for quantum computing.
I intend to use the wealth of PGM algorithms and tools to accelerate quantum computing research, by enabling programmers to ask new types of queries about quantum algorithms and programs. These approaches include:
- Using PGM knowledge compilation, a technique that enables efficient repeated inference, for more efficient simulation of near-term variational quantum algorithms that require repeated runs.
- Using PGM inference accelerator FPGA or ASIC hardware as a new way for classical hardware to support quantum program simulation.
- Using PGM sensitivity analysis, a way to tune PGMs to give correct inference results, as a technique to debug misbehaving quantum programs.
- Using PGM training algorithms as a model for understanding the correctness of near-term variational quantum algorithms.
These new approaches to analyzing quantum programs using classical computers would hasten the development of next-generation quantum computers and algorithms.
Research plan in analog co-processing for quantum control and measurement
As part of my five-year research plan, I see myself developing ways to use hybrid analog-digital computing to address challenges in quantum computer control and measurement. In current quantum computer architectures, a classical digital computer is in charge of interpreting quantum program instructions, which are then read from lookup tables into analog-to-digital converters to create analog control pulses. The aforementioned classical processing occurs at room temperature, while the actual quantum computing devices reside in a cold vacuum maintained by nested dilution refrigerators. The power dissipation of digital control processors limits how much classical processing can occur in close proximity to the quantum devices, thereby limiting the information bandwidth and interaction between the two systems. I suspect the low-power advantages of analog co-processing can help move classical control and measurement of the quantum information closer in proximity to the quantum devices. In such a scheme, the digital control processor phrases control signals as sparse parameters to nonlinear ODEs, which are then generated by a programmable analog device at minimal power dissipation next to the quantum devices. Historical ideas in analog computing may end up finding their most important use in future quantum computing systems!
Broader view: emerging architectures for the post-Moore’s Law era of computing
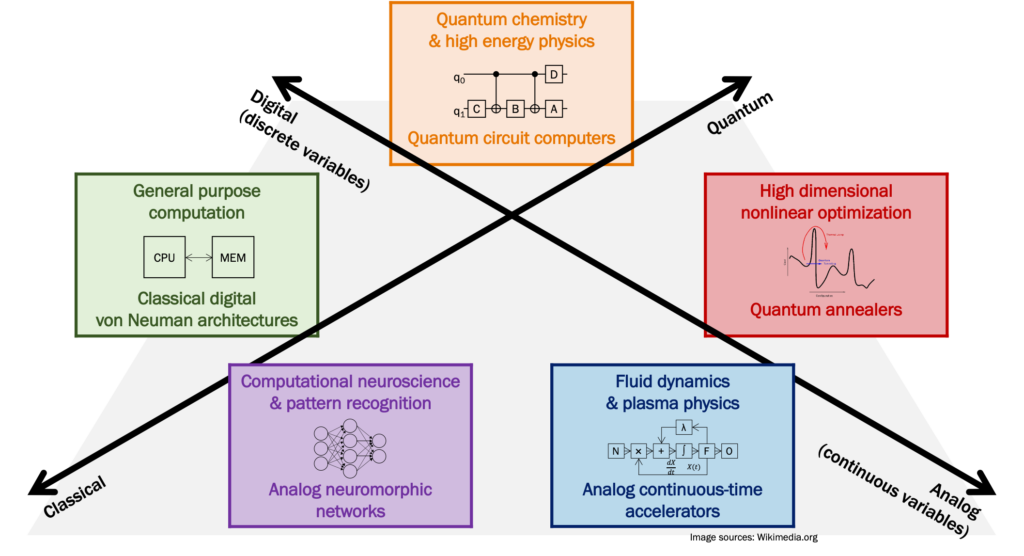
Going forward, computer application trends will increasingly create problems that strain von Neumann, digital, and classical computer architectures as we know them. In my research, I’ve met fluid dynamicists, plasma physicists, and quantum engineers who have computational problems so severe that they are seeking electrical engineers, material scientists, and physicists to create exotic computational devices to solve their problems. Within computer engineering, mainstream computing systems have rapidly diversified to include CPUs, GPUs, FPGAs, ASICs, and useful models of computation have expanded to include neural networks, analog accelerators, and quantum computers. My research addresses the challenges in identifying, building, evaluating, and finding correct abstractions to help us understand and safely use these emerging architectures.